Batch 2 - Class 89 - Locker Problem
Pre-Class Problem: (Carried forward as homework for this class)
Attendance: Anisha, Muskaan, Tishyaa, Adit, Diya, Nandini, Liza, Arnav, Anishka, Navya, Avy
Class Notes:
Locker Problem
Teacher's Notes: Ensure all students know about factors
One hundred students are assigned lockers 1 to 100. The student assigned locker number 1 goes through and opens all lockers. The student assigned 2 then closes all the lockers whose numbers are multiples of 2. Student assigned number 3 then changes the status of all lockers which are multiples of 3, and so on.
- Which lockers will be left open at the end?
- Answer: 1,4,9,16,25,36,49,64,81,100
- Can you explain why the above were left open?
- Answer: The open lockers are perfect squares. Why? Because they have odd number of factors
- Teacher's Notes: Let students come up with this observation. They may come up with the notion that only odd/even nature matters, or that the order in which students go is not important
- How many, and which lockers are touched exactly twice?
- Answer: Prime numbers, since they have only two factors
- Teacher's Notes: By this time, students should start to correlate number of factors to the number of toggles. And hence numbers with even number of factors being closed.
- Which students touched both lockers 36 and 48? How do you know?
- Answer: 1,2,3,4,6 and 12 - these are common factors of 36 and 48
Teacher's Notes: The following section may be accessible by kids who know prime factorization
- How does prime factorization and number of factors of a number relate? Try this out with a few numbers. First try with numbers with only one prime factor, such as 8, 9. Then try with numbers with multiple prime factors.
- Answer: Number of factors is 1 more than the exponent on the prime number in prime factorization. If a number has more than one prime factor, then it is the product of (1+ respective exponents). Why?
- Can you calculate the number of factors of 432?
- Answer: 432 = 2^4.3^3, so number of factors is 5.4=20
- Will 432 be open or closed in the locker problem?
More patterns
- What would happen in locker problem if only the even numbered students went across?
- What if only the primes went across?
- Given the set of people who walked, what is the general strategy for figuring out which lockers are open?
Inverting the problem
Can you describe which people should walk across if you want the following lockers to be open
- Only number 1
- Answer: 1 must be present. Then only numbers which have odd number of factors, counting only the students present, must be open. If you draw the pattern, you will notice that students present must be these which do not have repeated factors, also called "squarefree" numbers.
- All odds are open
- Answer: 1 must be present. Then 2 must be present to close 2. And so on. Draw the pattern.
- Given the lockers that are to be open, is there a general strategy to figure out which students must be present?
- For any set of lockers given to be open, is there necessarily a set of students present which will lead to that result? Can you prove or provide a counter-example?
Homework
Mirror Maze
Given a square grid, width some squares blocked and some occupied by mirrors, the task is to travel through all the available cells without crossing the itinerary.
The rules are as follows:
- You may not enter a blocked cell, which is filled with a solid square;
- You may enter the square with a thin mirror (shown with a slash or a back slash) twice without crossing the slash;
- You may enter the half solid mirror (shown as a painted triangle) only once through a non-painted part of it.

Note that you can not hit and reflect off the non-inclined sides of triangle or square. This Puzzle's task is to visit all of the vacant cells of the game field by drawing a closed line which does not cross itself. Example below:

Hint:
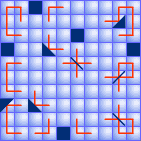
Lets solve for a few:



References: